Что называется осевой симметрией

Зачем органы дублируются?

Раз уж зашел разговор о дублировании органов, то стоит коротко упомянуть о причинах этого

Начнем снаружи – зачем человеку два уха? Для красоты и симметрии? Вовсе нет! Оказывается, в зависимости от того, до какого уха звук доходит раньше, а до какого на мгновение позже, человек подсознательно определяет, откуда именно он исходит! Это важно сегодня, а уж для пещерного человека, которого повсюду подстерегали опасности, а охота была главным источником еды, такой инструмент был неоценимым

То же самое про глаза. Посаженные на некотором расстоянии друг от друга, они позволяют более-менее точно определять дистанцию до объектов. Не верите? Попробуйте прикрыть один глаз ладонью и, пройдя через всю комнату, взять мелкий предмет с полки. Вовсе не факт, что получится сделать это с первого раза!

Почки дублируются просто потому, что именно на них приходится одна из самых больших нагрузок в теле человека. За сутки они фильтруют тонны крови! То есть, одни и те же пять литров крови (ну, плюс-минус поллитра, в зависимости от состояния и комплекции человека) проходит сотни и даже тысячи раз! Одна почка никак не справилась бы.

Дублирующееся сердце? Для человека – серьезное отклонение, а вот у осьминога их даже не два, а целых три! Причем расположены они очень близко друг к другу. Только таким путем он может создать достаточное давление в щупальцах – на большой глубине, да ещё и без костей это является наиболее рациональным решением, к какому пришла эволюция за миллионы лет.

Подписи к слайдам:

Слайд 1

Слайд 2

План урока Теоретическая самостоятельная работа с самопроверкой. Изучение нового материала с использованием презентации. Закрепление нового материала с использованием презентации.

Слайд 3

Ответы к тесту Вариант №1. Ч В заданиях вставьте пропущенные слова в определениях и теоремах. 1. *** называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. а) прямоугольник б) трапеция в) ромб г) четырехугольник 2.Прямоугольник – это ***, у которого все углы прямые. а) трапеция б) четырехугольник в) ромб г) параллелограмм 3. Диагонали ромба являются *** его углов. а) медианами б) высотами в) средними линиями г ) биссектрисами 4. *** называется четырехугольник, у которого только две противолежащие стороны параллельны. а) прямоугольник б) параллелограмм в) трапеция г) ромб 5. У параллелограмма противолежащие стороны равны, противолежащие *** равны. а) вершины б) углы в) прямые г) отрезки 6. Ромб – это ***, у которого все стороны равны. а) четырехугольник б) прямоугольник в) квадрат г) параллелограмм 7. *** параллелограмма пересекаются и точкой пересечения делятся пополам. а) вершины б) стороны в) углы г) диагонали 8. Диагонали *** равны. а) четырехугольника б) ромба в) прямоугольника г) трапеции Вариант №2. В заданиях вставьте пропущенные слова в определениях и теоремах. 1. *** называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. а) четырехугольник б) трапеция в) ромб г) прямоугольник 2.Прямоугольник – это ***, у которого все углы прямые. а) трапеция б) параллелограмм в) ромб г) четырехугольник 3. Диагонали ромба являются *** его углов. а) медианами б) высотами в) биссектрисами г) средними линиями 4. *** называется четырехугольник, у которого только две противолежащие стороны параллельны. а) прямоугольник б ) трапеция в) параллелограмм г) ромб 5. У параллелограмма противолежащие стороны равны, противолежащие *** равны. а) вершины б) отрезки в) прямые г) углы 6. Ромб – это ***, у которого все стороны равны. а) параллелограмм б) прямоугольник в) квадрат г) четырехугольник 7. *** параллелограмма пересекаются и точкой пересечения делятся пополам. а) вершины б) диагонали в) углы г) стороны 8. Диагонали *** равны. а) четырехугольника б ) прямоугольника в) ромба г) трапеции

Слайд 4

Ответы к тесту Вариант №1. 1 г 2 г 3 г 4 в 5 б 6 г 7 г 8 в Вариант №2. 1 а 2 б 3 в 4 б 5 г 6 а 7 б 8 б

Слайд 5

Центральная и осевая симметрии

Слайд 7

Точки А и А 1 называются симметричными относительно точки О , если О — середина отрезка АА 1 . О — центр симметрии А А 1 О Точка О считается симметричной самой себе. Центральная симметрия

Слайд 8

Какие из точек симметричны относительно точки О ? N N 1 О M M 1 Q P

Слайд 9

Задание1 Построить треугольник, симметричный АВС относительно точки О . О В А С А 1 С 1 В 1 Построение.

Слайд 10

Фигура называется симметричной относительно точки О , если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. О О Примеры фигур, имеющих центр симметрии. О О

Слайд 11

Осевая симметрия Две точки А и А 1 называются симметричными относительно прямой n , если эта прямая проходит через середину отрезка АА 1 и перпендикулярна к нему. n А А 1 n – ось симметрии О

Слайд 12

Какие из точек симметричны относительно прямой b ? b N N 1 M M 1 A A P

Слайд 13

b С В А А 1 В 1 С 1 Задание 2 Построить треугольник, симметричный АВС относительно прямой b Построение.

Слайд 14

Фигура называется симметричной относительно прямой n , если для каждой точки фигуры симметричная ей точка относительно прямой n также принадлежит этой фигуре. Примеры фигур, имеющих ось симметрии.

Слайд 15

Примеры фигур, обладающих центральной и осевой симметрией.

Почему лицо не симметрично?

Однако, говоря о симметричности, не стоит забывать и об определенных отклонениях. Возможно, многим приходилось слышать о том, что на самом деле левая и правая части тела человека не абсолютно симметричны. Причем речь идет не о внутреннем строении, при котором левая и правая почки имеют разную форму, причем одна расположена чуть ниже другой. И не о том, что сердце расположено слева, а печень – справа.

На самом деле определенная асимметрия присуща человеку в целом. Самое простое – правая рука в большинстве случаев сильнее и, как следствие, мышцы здесь толще. Ничего странного здесь нет – ведь правши используют правую руку чаще, а значит она будет более развитой.

Но куда более интересной является асимметрия лица. Ваше лицо симметрично? Как бы не так! У подавляющего большинства людей левая и правая стороны немного отличаются. И речь не о родинках или других бросающихся в глаза различиях. Просто половинки лица не симметричны. Если провести эксперимент, отразив в фоторедакторе любую свою портретную фотографию, и склеить половинки между собой, то можно прийти к удивительному результату. Лицо будет до боли знакомым, но это уже не ваше лицо!

Сложно сказать, почему же это так. Возможно, это связано с тем, что многие люди чаще жуют пищу на одной стороне челюсти, а не равномерно. Из-за этого мышцы развиваются не совсем идентично. Но ученые пока не могут ответить достоверно на этот необычный и интересный вопрос. А некоторые наблюдательные люди утверждают, что у детей это различие более заметно, чем у взрослых. То есть, с возрастом черты лица сглаживаются и половинки становятся больше похожи одна на другую.

О центральной и осевой симметрии

В математике выделяют такие ее виды:

• центральная, то есть выполненная относительно одной точки;
• осевая, которая наблюдается около прямой;
• зеркальная, она основывается на отражениях;
• симметрия переноса.

Что такое ось и центр симметрии? Это точка или прямая, относительно которой любой точке тела найдется другая. Причем такая, чтобы расстояние от исходной до получившейся делилось пополам осью или центром симметрии. Во время движения этих точек они описывают одинаковые траектории.

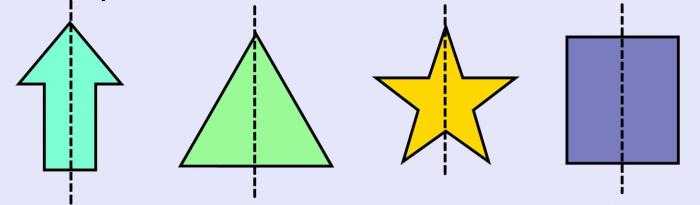
В ситуациях, когда необходимо найти центр симметрии, нужно поступать следующим образом. Если фигур две, то найти у них одинаковые точки и соединить их отрезком. Потом разделить пополам. Когда фигура одна, то помочь может знание ее свойств. Часто этот центр совпадает с точкой пересечения диагоналей или высот.

Фигуры, имеющие несколько осей симметрии

Две оси симметрии характерны для прямоугольника. Это прямые, которые проведены через точки, являющиеся серединами его противоположных сторон.

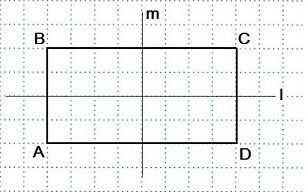
То же самое (наличие двух осей) присуще и ромбу. Оси являются прямыми, содержащими диагонали данной геометрической фигуры.

Интерес представляет и квадрат, у которого насчитывается четыре оси. Данная фигура является одновременно и ромбом, и прямоугольником. Остальные виды параллелограммов не имеют осей симметрии вообще.

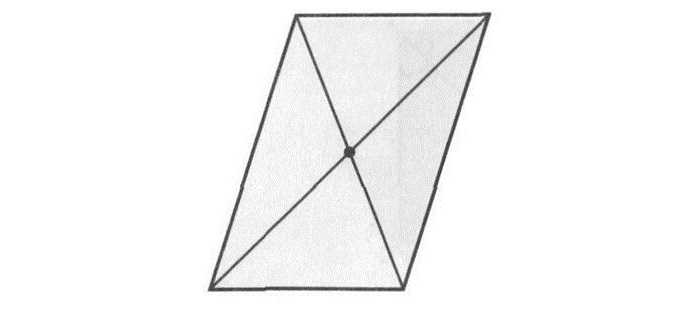
Рис. 5 Оси симметрии ромба

Единственной фигурой, у которой есть три оси симметрии, является равносторонний треугольник. Они представляют собой не что иное, как его медианы, линии соединяющие середины его сторон. Медианы равностороннего треугольник – это его и биссектрисы, и высоты.

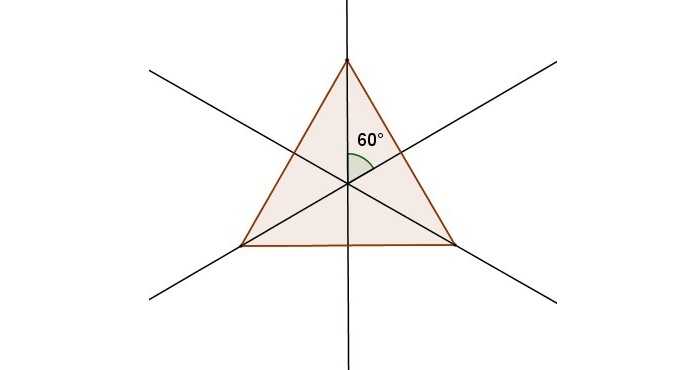
Рис. 6 Оси симметрии равностороннего треугольника

В обычной жизни многие даже не задумываются о том, как часто они сталкиваются с различными видами симметрии. Это понятие характерно не только для мира математики. 

Симметрия встречается в мире природы, архитектуре, в мире искусства и композиции, а также в других сферах человеческой жизни.

Осознание данного факта прошло долгий путь во времени, над ним задумывались великие умы на протяжении многих столетий. С древних времен и до настоящего времени определение этого понятия прошло долгий путь развития.

Что такое центральная симметрия

Точки А и А1 называются симметричными относительно точки О, если О — середина АА1.

Рисунок 1. Центральная симметрия в снежинке. 

Например, центр симметрии:

• окружности — центр окружности;
• параллелограмма — точка пересечения его диагоналей;
• прямой — любая точка прямой, то есть бесконечное множество центров симметрии.

Фигуру можно называть симметричной относительно центра симметрии, если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре. 

Фигуры, симметричные относительно некоторой точки, равны. 

Одним из первых ученых, подробно изучавшим центральную симметрию, был выдающийся немецкий математик Феликс Клейн. При изучении геометрии, утверждал Клейн, нужно рассматривать не только объекты (треугольники, окружности и т.д.), но и перемещения.

В классической геометрии Евклида более двух тысяч лет под перемещениями понимались только движения твердого тела: можно взять фигуру и поместить ее копию в новое место. При подходе Клейна геометрия охватывает гораздо более широкий класс задач, чем в классическом понимании. 

1. Доказательство с помощью векторов: Пусть точки A и B отобразились соответственно на A1 и B1, а О — центр симметрии. Тогда, из определения центральной симметрии, векторы OA1 = -OA, OB1 = -OB.

Рассмотрим вектор A1B1 = OB1 — OA1= -(OB)-(-OA)= -OB+OA= -(OB-OA)= -AB.

Следовательно, центральная симметрия является движением, изменяющим направление на противоположное.

2. Доказательство геометрическим методом. 

Дано: точки А и В, точка О — центр, А1, В1 — образы исходных точек, АО=ОА1, ВО=ОВ1. 

Доказать, что АВ=А1В1. 

Рисунок 2. 

Решение: 

Рассмотрим ΔAOB и ΔA1OB1 (рисунок 2). По условию: 

1. AO=A1O.
2. BO=B1O.
3. 3. ∠AOB=∠A1OB1, так как это вертикальные углы.

1,2,3 ⇒ ΔAOB = ΔA1OB ⇒ AB=A1B1. Что и требовалось доказать. 

Свойства центральной симметрии

Основные свойства следующие:

1. Центральную симметрию называют движением, при котором соответствующие точки также остаются симметричными, то есть расстояние между ними остаётся прежним.

Посмотрим на рисунок. Треугольники АВС и А₁В₁С₁
симметричны в пространстве относительно точки О. При каком либо преобразовании пространства сохраняются условия: АО=А₁О, ВО=В₁О, СО=С₁О. Значит, картинка остаётся той же.

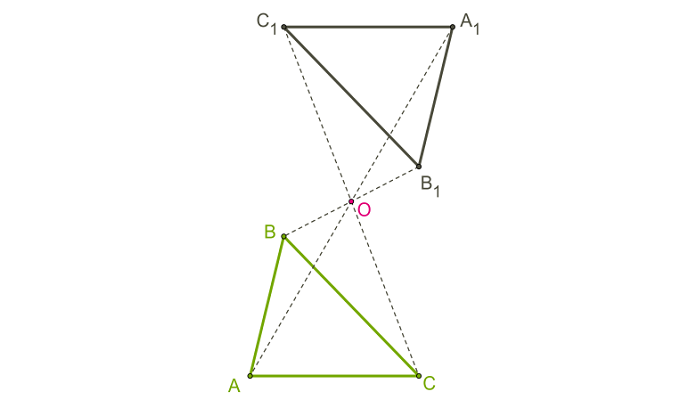
Однако если представить геометрическую фигуру в виде векторов, то при преобразовании пространства эти векторы поменяют свои направления;

2. Центральная симметрия имеет только одну центральную точку, которая является неподвижной при преобразовании пространства;

3. Если прямая проходит через центр симметрии, то она соответствует самой себе, то есть симметрична;

4. Центральная симметрия переводит прямую, не проходящую через центр симметрии, в параллельную ей прямую.

Доказывается это свойство достаточно просто. Для этого нужно построить две параллельные прямые АВ и А₁В₁ относительно точки О_.

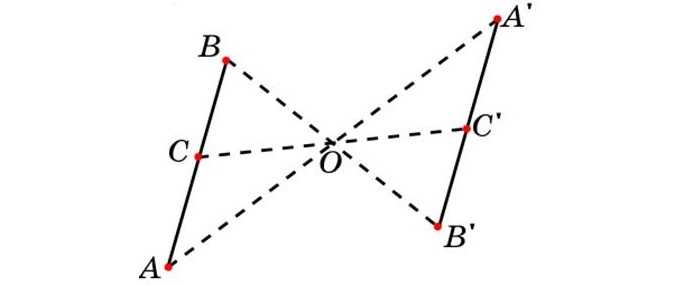
Далее соединяем симметричные точки и получаем отрезки АА₁ и ВВ₁. Далее легко заметить, что отрезки АО и А₁О будут равны. Соответственно равны и отрезки ВО и В₁О. Углы, которые образуются при пересечении двумя прямыми точки О также равны. 

Значит, треугольники равны по двум сторонам и углу между ними. Следовательно, равны углы А,А₁ и В,В_1. Значит они являются накрест лежащими при секущих АА₁ и ВВ₁. Задача решена, АВ и А₁В₁ параллельны;

5. При центральной симметрии отрезки симметричны отрезкам, лучи симметричны лучам, прямые симметричны прямым.

Пару слов о симметричности

Для начала стоит разобраться, что же подразумевается под этим термином. Тут все довольно просто – левая часть любого существа очень похожа на правую. Возможно, внутри есть определенные неточности, но внешне о них сложно догадаться.

Симметрия бывает двух типов – радиальная и билатеральная. Первая присуща для примитивных существ, вроде морских звезд, гидр и актиний. Ну и конечно, в эту же категорию можно отнести одноклеточные организмы, которые вообще имеют практически округлую форму. Их всех можно разделить условными осями на несколько частей, которые будут совершенно одинаковыми.

С билатеральной симметрией все ещё проще – её также называют зеркальной. И ею обладает большинство обитателей планеты Земля – все птицы, рыбы, животные и, разумеется, человек. Впрочем, здесь есть несколько исключений. Например, камбала – у неё левая часть слабо похожа на правую. Или манящий краб, у которого одна клешня всегда значительно крупнее, чем другая. Но эти исключения единичны, и они скорее подтверждают правило, чем опровергают его.

Интересные факты о центральной симметрии

Вся окружающая нас природа – сплошная центральная симметрия. Многие растения и насекомые обладают центральной симметрией. 

Практически у каждого фрукта есть своя симметрия. Например, кокос в разрезе представляет собой окружность с центром в некоторой точке. 

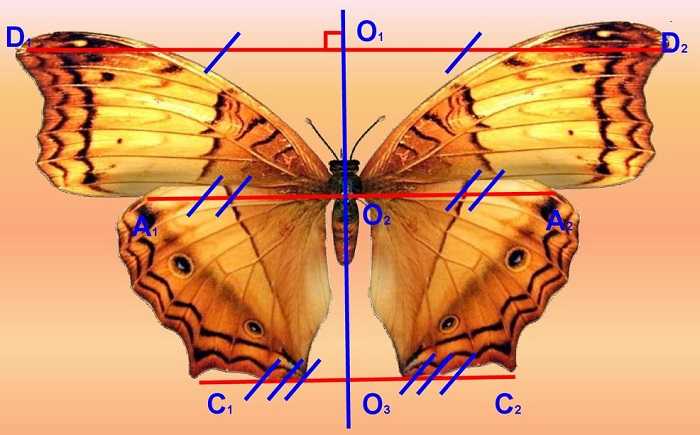
Ещё один очевидный пример – бабочка. 

Великолепные узоры на её крылышках – четкая и яркая симметрия. 

Каждый знает, что видовое разнообразие морских ракушек бесконечно. Наверняка, вы сможете найти несколько как с осевой, так и центральной симметрией.

Великолепные примеры с элементами центральной симметрии можно наблюдать и в архитектуре. Потолки различных храмов и церквей украшаются орнаментами, основой которых является центральная симметрия. 

Собор Парижской Богоматери имеет прекрасный, утончённый узор, основанный на центральной симметрии.

Рукодельницы в своих произведениях искусства применяют симметрию, которая заметна в удивительных и затейливых узорах.

Таким образом, центральная симметрия – основа, которая составляет природу, архитектуру и даже иногда музыку. Именно это проявление так радует человеческий глаз при появлении первых снежинок или при знакомстве с сооружениями архитектуры.

Симметрия в повседневной жизни

Симметрия стала частью жизни человека уже в древние времена. Орнаменты с признаками зеркального отражения встречаются на античных зданиях, древнегреческих вазах. Свойство пропорционального расположения заимствовано в науку из природы. 

Зеркальное отражение часто встречается в живой и неживой природе. Этой характеристикой обладают снежинки. В растительном мире одинаково расположены противоположные элементы растений: большинство листьев зеркально отражаются сравнительно среднего стебля. В животном мире законы симметрии проявляются в наличии у животных правой и левой сторон. Большинство представителей фауны обладает парными частями тела: уши, лапы, глаза, крылья, рога. Ярким образцом зеркальной симметрии считается бабочка. Прямая, условно проведенная вдоль туловища насекомого по центру, является осью симметрии.

Поскольку человек – это часть природы, в своем творчестве он использует принцип симметрии. В искусстве свойство отражения применяется для создания красоты и гармонии. В архитектуре пропорциональность выполняет практическую функцию – придает зданиям устойчивость и надежность. В предметах быта можно встретить одинаковость в расположении частей узоров на коврах, принтов на ткани, рисунков обоев.

Дискретные группы симметрии

Эти аффинные симметрии можно рассматривать как предельные случаи :

Группа	Coxeter	Описание
C∞	+		Циклический: ∞-кратные вращения становятся трансляциями. Абстрактная группа Z∞, то бесконечная циклическая группа.
D∞			Двугранные: ∞-кратные отражения. Абстрактная группа Dih∞, то бесконечная диэдральная группа.

Трансляционная симметрия

Рассмотрим все шаблоны в 1D, которые имеют трансляционные симметрия, т.е. функции ж(Икс) такой, что для некоторых а > 0, ж(Икс + а) = ж(Икс) для всех Икс. Для этих паттернов значения а для которых это свойство имеет место группа.

Сначала рассмотрим паттерны, для которых группа дискретный, т. е. для которых положительные значения в группе имеют минимум. При изменении масштаба мы делаем это минимальное значение равным 1.

Такие модели делятся на две категории: две одномерные. космические группы или же группы линий.

В более простом случае единственные изометрии р которые сопоставляют шаблон с самим собой, являются переводами; это применимо, например, к шаблону

− −−−  − −−−  − −−−  − −−−

Каждая изометрия может быть охарактеризована целым числом, а именно плюс или минус расстояние перемещения. Следовательно группа симметрии является Z.

В другом случае среди изометрий р которые отображают узор на себя, также есть отражения; это применимо, например, к шаблону

− −−− −  − −−− −  − −−− −

Выбираем происхождение для Икс в одной из точек отражения. Теперь все отражения, которые отображают узор на себя, имеют форму а−Икс где постоянная «а«является целым числом (приращение а снова равны 1, потому что мы можем объединить отражение и перевод, чтобы получить другое отражение, и мы можем объединить два отражения, чтобы получить перевод). Следовательно, все изометрии можно охарактеризовать целым числом и кодом, скажем 0 или 1, для перевода или отражения.

Таким образом:

• (а,)Икс↦Икс+а{ Displaystyle (а, 0): х mapsto х + а}
• (а,1)Икс↦а−Икс{ Displaystyle (а, 1): х mapsto а-х}

Последний является отражением относительно точки а/ 2 (целое число или целое число плюс 1/2).

Групповые операции (функциональная композиция, первый справа) для целых чисел а и б:

• (а,)∘(б,)=(а+б,){ displaystyle (a, 0) circ (b, 0) = (a + b, 0)}
• (а,)∘(б,1)=(а+б,1){ displaystyle (a, 0) circ (b, 1) = (a + b, 1)}
• (а,1)∘(б,)=(а−б,1){ displaystyle (a, 1) circ (b, 0) = (a-b, 1)}
• (а,1)∘(б,1)=(а−б,){ displaystyle (a, 1) circ (b, 1) = (a-b, 0)}

Например, в третьем случае: перевод на сумму б изменения Икс в Икс + ботражение относительно 0 дает —Икс − б, и перевод а дает а − б − Икс.

Эта группа называется из Z, Dih (Z), а также D_∞. Это полупрямой продукт из Z и C₂. Оно имеет нормальная подгруппа из индекс 2 изоморфен Z: переводы. Также он содержит элемент ж порядка 2 такой, что для всех п в Z,  п ж = ж п −1: Отражение относительно опорной точки, (0,1).

Эти две группы называются группы решеток. В решетка является Z. В качестве трансляционной ячейки можно взять интервал 0 ≤ Икс фундаментальная область можно взять то же самое; топологически это круг (1-тор); во втором случае можно взять 0 ≤ Икс ≤ 0.5.

Настоящий дискретная симметрия группа трансляционно-симметричного узора может быть:

• типа группы 1 для любого положительного значения наименьшего расстояния перевода
• типа группы 2, для любого положительного значения наименьшего трансляционного расстояния и любого расположения решетки точек отражения (которая вдвое плотнее, чем трансляционная решетка)

Таким образом, набор трансляционно-симметричных паттернов можно классифицировать по фактическим группам симметрии, в то время как фактические группы симметрии, в свою очередь, можно классифицировать как тип 1 или тип 2.

Эти типы пространственных групп представляют собой группы симметрии «с точностью до сопряженности относительно аффинных преобразований»: аффинное преобразование изменяет расстояние трансляции на стандартное (см. Выше: 1) и положение одной из точек отражения, если применимо, к происхождению. Таким образом, реальная группа симметрии содержит элементы вида кляп−1= б, который является конъюгатом а.

Недискретные группы симметрии

Для однородного «паттерна» группа симметрии содержит все трансляции и отражение во всех точках. Группа симметрии изоморфна Dih (р).

Существуют также менее тривиальные шаблоны / функции с трансляционной симметрией для произвольно малых переводов, например группа переводов на рациональные расстояния. Даже помимо масштабирования и смещения случаев существует бесконечно много, например рассматривая рациональные числа, знаменатели которых являются степенями данного простого числа.

Переводы образуют группу изометрий. Однако нет никакой закономерности с этой группой как группой симметрии.

Орбиты и стабилизаторы

Рассмотрим группу грамм действующий на множестве Икс. В точки Икс в Икс это набор элементов Икс которому Икс могут перемещаться элементами грамм. Орбита Икс обозначается Gx:

граммИкс={грамм⋅Икс∣грамм∈грамм}.{ Displaystyle Gx = left {g cdot x mid g in G right }.}

Случай, когда групповое действие включено р:

Для тривиальной группы все орбиты содержат только один элемент; для группы переводов орбита равна, например, {.., — 9,1,11,21, ..}, для отражения, например {2,4}, а для группы симметрии со сдвигами и отражениями, например, {−8, −6,2,4,12,14,22,24, ..} (расстояние переноса равно 10, точки отражения .., — 7, −2,3,8,13,18,23, ..). Точки на орбите «эквивалентны». Если к узору применяется группа симметрии, то внутри каждой орбиты цвет будет одинаковым.

Дело в том, что групповое действие происходит по шаблонам:

Орбиты представляют собой наборы шаблонов, содержащие переведенные и / или отраженные версии, «эквивалентные шаблоны». Перевод шаблона эквивалентен только в том случае, если расстояние перевода является одним из тех, которые включены в рассматриваемую группу симметрии, и аналогично для зеркального отображения.

Множество всех орбит Икс под действием грамм записывается как Икс/грамм.

Если Y это подмножество из Икс, мы пишем GY для набора {грамм · у : у ∈{ displaystyle in}Y и грамм ∈{ displaystyle in}грамм}. Мы называем подмножество Y инвариантен относительно G если GY = Y (что эквивалентно GY ⊆ Y). В таком случае, грамм также работает на Y. Подмножество Y называется фиксируется под G если грамм · у = удля всех грамм в грамм и все у в Y. В примере с орбитой {−8, −6,2,4,12,14,22,24, ..}, {−9, −8, −6, −5,1,2,4,5, 11,12,14,15,21,22,24,25, ..} инвариантно относительно грамм, но не исправлено.

Для каждого Икс в Икс, мы определяем подгруппа стабилизатора из Икс (также называемый группа изотропии или же маленькая группа) как набор всех элементов в грамм это исправление Икс:

граммИкс={грамм∈грамм∣грамм⋅Икс=Икс}.{ Displaystyle G_ {x} = {g in G mid g cdot x = x }.}

Если Икс — точка отражения, ее стабилизатор — группа второго порядка, содержащая тождество и отражение вИкс. В остальных случаях стабилизатор — тривиальная группа.

Для фиксированного Икс в Икс, рассмотрим карту из грамм к Икс данный грамм∣→грамм⋅Икс{ displaystyle g mid rightarrow g cdot x}. В изображение этой карты — орбита Икс и coimage это набор всего, что осталось смежные классы из грамм_Икс. Стандартная фактор-теорема теории множеств затем дает естественное биекция между граммграммИкс{ displaystyle G / G_ {x}} и граммИкс{ displaystyle Gx}. В частности, биекция дается формулой часграммИкс∣→час⋅Икс{ displaystyle hG_ {x} mid rightarrow h cdot x}. Этот результат известен как теорема о стабилизаторе орбиты. Если в примере взять Икс=3{ displaystyle x = 3}, орбита {−7,3,13,23, ..}, и эти две группы изоморфны Z.

Если два элемента Икс{ displaystyle x} и у{ displaystyle y} принадлежат одной орбите, то их стабилизирующие подгруппы, граммИкс{ displaystyle G_ {x}} и грамму{ displaystyle G_ {y}}, находятся изоморфный. Точнее: если у=грамм⋅Икс{ Displaystyle у = г cdot х}, тогда грамму=граммграммИксграмм−1{ displaystyle G_ {y} = gG_ {x} g ^ {- 1}}. В примере это применимо, например, для 3 и 23 — обе точки отражения. Отражение около 23 соответствует переносу -20, отражение около 3 и переносу 20.

Причины симметричности

Чтобы разобраться, почему все организмы на планете Земля симметричны, придется отправиться в путешествие на миллиард лет назад, когда жизнь здесь только зародилась. Тогда в морях обитали только самые простейшие существа. Разумеется, они были совершенно симметричными – практически правильная окружность. Это позволяло им легко перемещаться в привычной среде обитания и обеспечивало хорошие шансы на выживание – как травоядным (точнее, водорослеядным), так и хищным.

Но эволюция вовсе не стоит на месте. Постепенно появлялись все более сложные организмы – сначала рыбы, затем амфибии, а затем и млекопитающие. Но привычная симметрия сохранялась. Для этого есть несколько причин. В первую очередь – обычное равновесие

Если в воде это не слишком важно, то на твердой земле, когда на любой объект действует довольно мощная сила тяжести, это становится очень серьёзным фактором

К тому же, многие части тела человека дублируются. Взять хотя бы глаза, уши, руки, ноги. Даже некоторые внутренние органы располагаются симметрично, вроде почек. Они имеют для организма одинаковую ценность. Поэтому должны одинаково снабжаться кровью, несущей питательные вещества и кислород

Из-за этого очень важно, чтобы они располагались примерно на одинаковом расстоянии от сердца. А уже это – прямой путь к зеркальной симметрии

Центральная симметрия

Это явление относительно некой точки. Она представляет собой преобразование множества точек пространства или поверхности, во время которого ее центр всегда постоянен и не меняет своего положения.

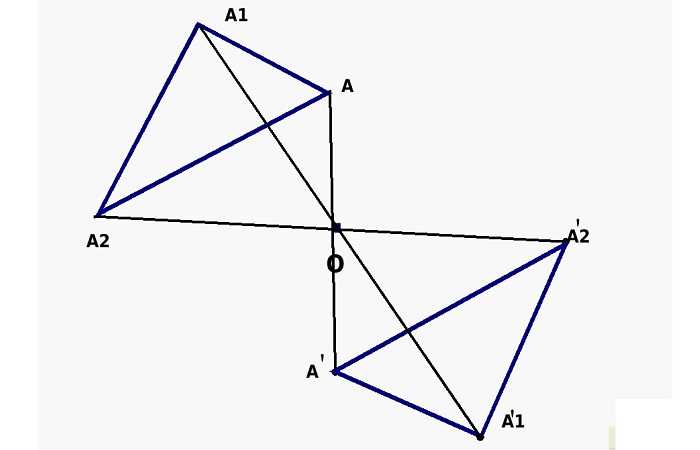
Данный вид симметрии предполагает, что на равном расстоянии от ее центра располагаются два предмета, например, две точки. Если провести между ними условную прямую, они будут располагаться на ее противоположных концах, а середина этой прямой и будет являться осевым центром. 

Если считать центр неподвижным и начать преобразовывать прямую (т. е. вращать ее относительно центральной точки), то точки на ее концах опишут две кривые. Все точки одной кривой будут иметь такие же симметричные точки на другой кривой.

Объекты, обладающие центром симметрии, представляют большой интерес для ученых. В геометрии насчитывается достаточно много таких объектов. К ним относятся прямые, отрезки, окружность, прямоугольник и др. Центрально симметричные объекты встречаются и в природе.

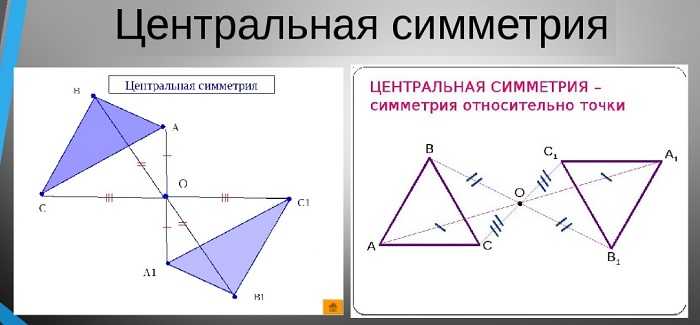
Рис. 2 Графическое представление центральной симметрии

Естествознание

§ 40. Симметрия в искустве и науке

Круг и квадрат — вот буквы алфавита
применяемые авторами в качестве
основы лучших произведений
К.-Н. Леду

Как проявляется симметрия в произведениях искусства? Какое значение в искусстве имеет симметрия? Какие научные выводы можно сделать на основе симметрии?

Урок-практикум

ЦЕЛЬ РАБОТЫ. На конкретных примерах, приведенных в параграфе, сделать выводы относительно роли симметрии в искусстве и науке.

ПЛАН РАБОТЫ

Последовательно выполняя задания, сформулируйте выводы о том, насколько важно чувство симметрии в искусстве, и о том, что может дать симметрия в естественных науках

1. Перед вами автопортрет французского художника XVII в. Н. Пуссена. Рассмотрите его. Как вам кажется на первый взгляд, можно ли назвать изображение симметричным? Приведите доказательства. А теперь попробуйте экспериментальным путем определить: где проходит ось симметрии? Обнаружили ли вы что-то странное? Предложите несколько вариантов ответа на вопрос: «Почему художник выбрал именно такое композиционное решение автопортрета?» Обсудите свое мнение с одноклассниками.

Никола Пуссен. Автопортрет

2. Приведите примеры симметрий в архитектуре. Что, по-вашему, имел в виду архитектор К.-Н. Леду, чье высказывание приведено в эпиграфе?

ПОДСКАЗКА. Круг и квадрат являются примерами симметричных фигур. В природе существует большое разнообразие симметричных объектов. Что значит симметрия некоторого объекта? Определение, которое мы дадим, не очень строгое, но простое для понимания. Если при некоторых преобразованиях объект переходит сам в себя, то он обладает свойствами симметрии относительно этих преобразований.

3. Изображение на картине Ж. Шардена «Медный бак» вообще кажется совершенно несимметричным, и все-таки здесь тоже есть симметрия. Чтобы убедиться в этом, проделайте несложный опыт. Сначала на иллюстрации прикройте изображение медного черпака с длинной ручкой (он изображен слева) и внимательно посмотрите на картину. Что произошло? Теперь повторите свои действия, но закройте глиняный кувшин или небольшую крышку, которые автор расположил на полу справа. Вновь рассмотрите изображение. Что произошло на этот раз? Осмыслите свои впечатления и постарайтесь определить, о каком виде симметрии зритель вправе говорить. Обоснуйте свою точку зрения.

Жан Шарден. Медный бак

Еще одним примером является сферически симметричный объект, который при поворотах на любой угол относительно любой оси, проходящей через центр симметрии, переходит сам в себя; примером может быть земной шар. Конечно же, земной шар лишь приближенно обладает сферической симметрией, однако в большинстве интересующих исследователей случаев это приближение достаточно хорошее.

Оказывается, что из симметрии объектов можно, не производя каких-либо расчетов, вывести много важных свойств. Попробуйте, выполнив следующее задание, доказать, что гравитационная сила, действующая на некоторый объект со стороны Земли, всегда направлена к центру земного шара.

4. Предположим, что сила притяжения направлена не к центру Земли (рис. 54, а). Мысленно поверните Землю вокруг оси, соединяющей центр Земли и точку А, на 180*. Объясните, почему при таком повороте вектор силы должен повернуться так, как это указано на рисунке 54, б. Вспомните определение симметричного объекта и, отталкиваясь от противного, сформулируйте доказательство того, что гравитационная сила направлена к центру Земли.

Рис. 54

ПОДСКАЗКА. Доказательство того, что гравитационная сила в законе всемирного тяготения убывает обратно пропорционально квадрату расстояния, также следует из симметрии, правда, это доказывается несколько сложнее.

Как уже говорилось, симметрия в микромире играет большую роль, чем в макромире и мегамире. Это объясняется несколькими причинами. Первая из них — точная симметрия микроскопических обьектов. Если земной шар лишь приближенно сферически симметричен, то свободный (ни с чем не взаимодействующий) атом имеет точную сферическую симметрию. Если макроскопическая гантель приближенно симметрична (вы сами можете попробовать установить, какие преобразования симметрии здесь имеют место), то эквивалентная ей по симметрии молекула водорода обладает точной симметрией.

Во-вторых, в микромире действует дополнительная симметрия, о которой мы уже говорили в § 26. Все одинаковые объекты микромира полностью тождественны.

Зная симметрию обьектов, можно вывести множество свойств этих объектов.

Что означает симметрия в разных науках?

Биология

В ней важной составляющей симметрии является то, что животные и растения имеют закономерно расположенные части. Причем в этой науке не существует строгой симметрии

Всегда наблюдается некоторая асимметрия. Она допускает то, что части целого не совпадают с абсолютной точностью.

Химия.

Физика. Система тел и изменения в ней описываются с помощью уравнений. В них оказываются симметричные составляющие, что позволяет упростить все решение. Это выполняется благодаря поиску сохраняющихся величин.

Математика. Именно в ней в основном и дается разъяснение, что такое симметрия. Причем большее значение ей уделяется в геометрии. Здесь симметрия — это способность к отображению у фигур и тел. В узком смысле она сводится просто к зеркальному отображению.